Polylabel

Polylabel.jl finds the pole of inaccessibility of a polygon, the most distant internal point from the polygon outline. This is useful for visual techniques like labelling polygons.

The main entry point is Polylabel.polylabel(polygon; atol, rtol) which processes any GeoInterface-compatible polygon (from GeometryBasics.jl, ArchGDAL.jl, LibGEOS.jl, Shapefile.jl, etc.) and returns a point as a 2-tuple of (x, y). It uses GeometryOps.jl to compute distances.

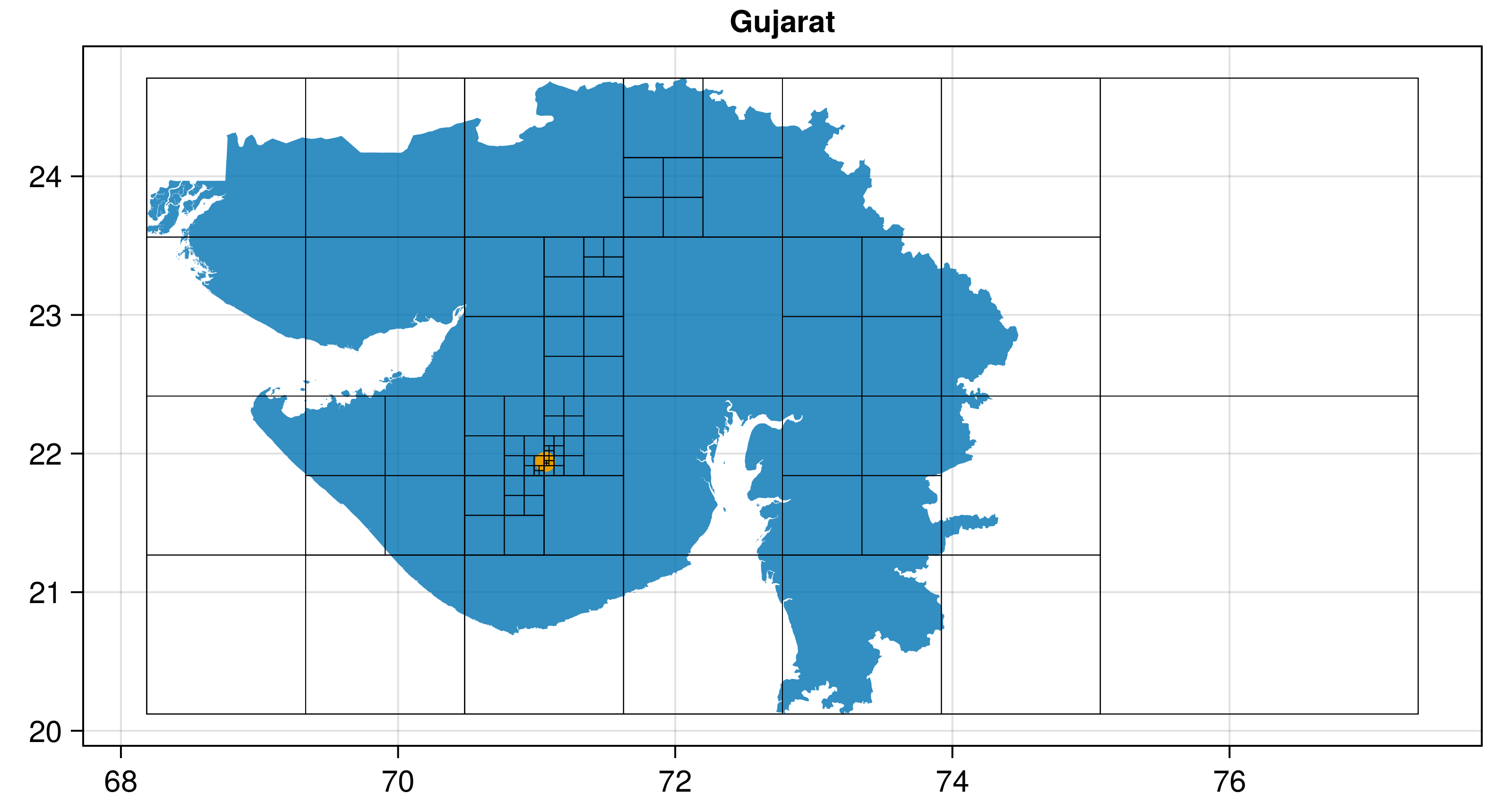
This algorithm was originally written (and taken from) mapbox/polylabel - you can find a lot more information there! To summarize, the algorithm is basically a quad-tree search across the polygon which finds the point which is most distant from any edge.

There is an alternative Julia implementation of this algorithm in DelaunayTriangulation.jl

Tutorial

Polylabel is mostly used to find the optimal point to place a label for a polygon. So let's label the provinces of France!

First, we'll get the data using GADM.jl (but you can load any dataset or even just a custom vector of geometries).

This is basically a dataframe with a column of polygons (:geom) and a column of names (:NAME_1), plus some other stuff.

using GADM, DataFrames
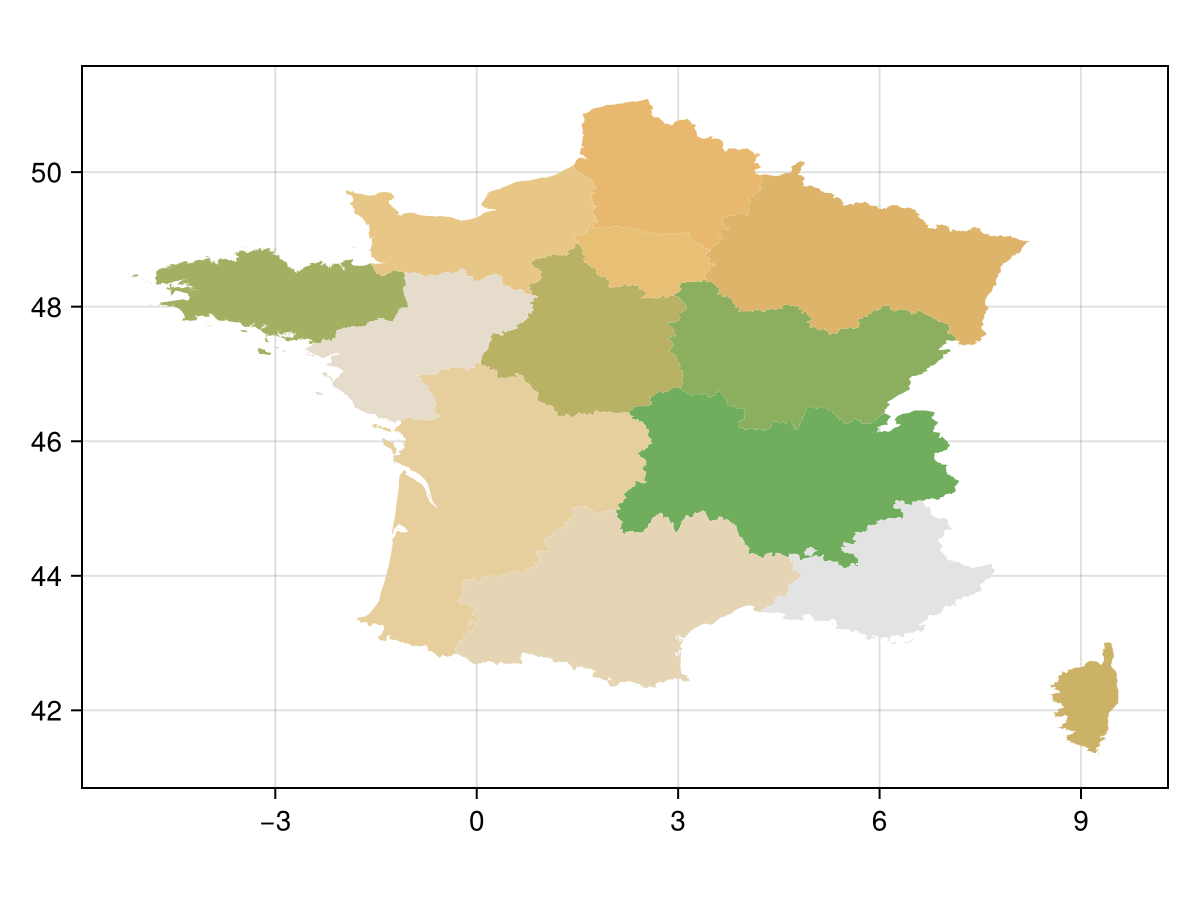
fra_states = GADM.get("FRA"; depth = 1) |> DataFrame

Now, let's plot the geometries using Makie.jl.

using CairoMakie, GeoInterfaceMakie
f, a, p = poly( # the `poly` recipe plots polygons
    fra_states.geom;
    color = 1:size(fra_states, 1),  # this can be anything
    colormap = :linear_gow_65_90_c35_n256,
    axis = (; aspect = DataAspect())
)

Now, we actually get the polylabel points. Note that this is the only point in this entire tutorial, in which we've used the package!

using Polylabel
label_points = polylabel.(fra_states.geom) # broadcast across array of polygons

13-element Vector{Tuple{Float64, Float64}}:
 (4.609312265740437, 45.27603623375587)
 (4.399733693283226, 47.14209052905285)
 (-3.2311704373591574, 48.277860622140665)
 (1.6292935682617864, 47.39589805073056)
 (9.109488690701287, 42.24161942968179)
 (4.810991063687439, 48.89094670243756)
 (2.6722452357071242, 49.919972509550846)
 (2.710264533648551, 48.62878850119535)
 (0.8581305739200004, 49.29945222296688)
 (0.4018724950254621, 45.56928741724809)
 (1.8283359174514129, 43.65198697933018)
 (-0.4062326557888818, 47.7859534460392)
 (6.337364444089905, 43.96619612654306)

Let's also show these obtained points on the plot:

sp = scatter!(a, label_points; color = (:red, 0.3))
f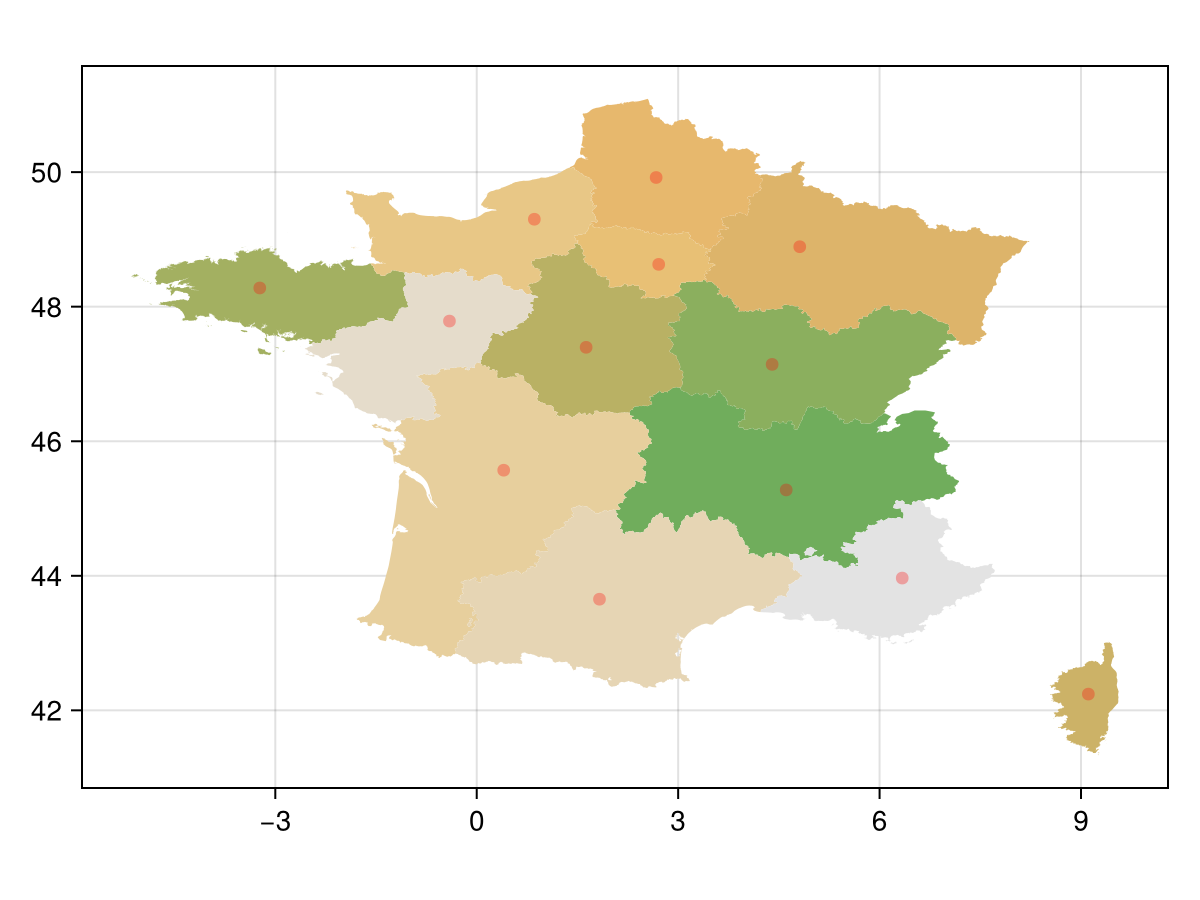

Finally, we'll plot actual labels for the provinces as text:

labelplot = text!(
    a, label_points;
    text = fra_states.NAME_1,
    align = (:center, :center),
    fontsize = 10,
    strokecolor = :white,
    strokewidth = 0.1
)

f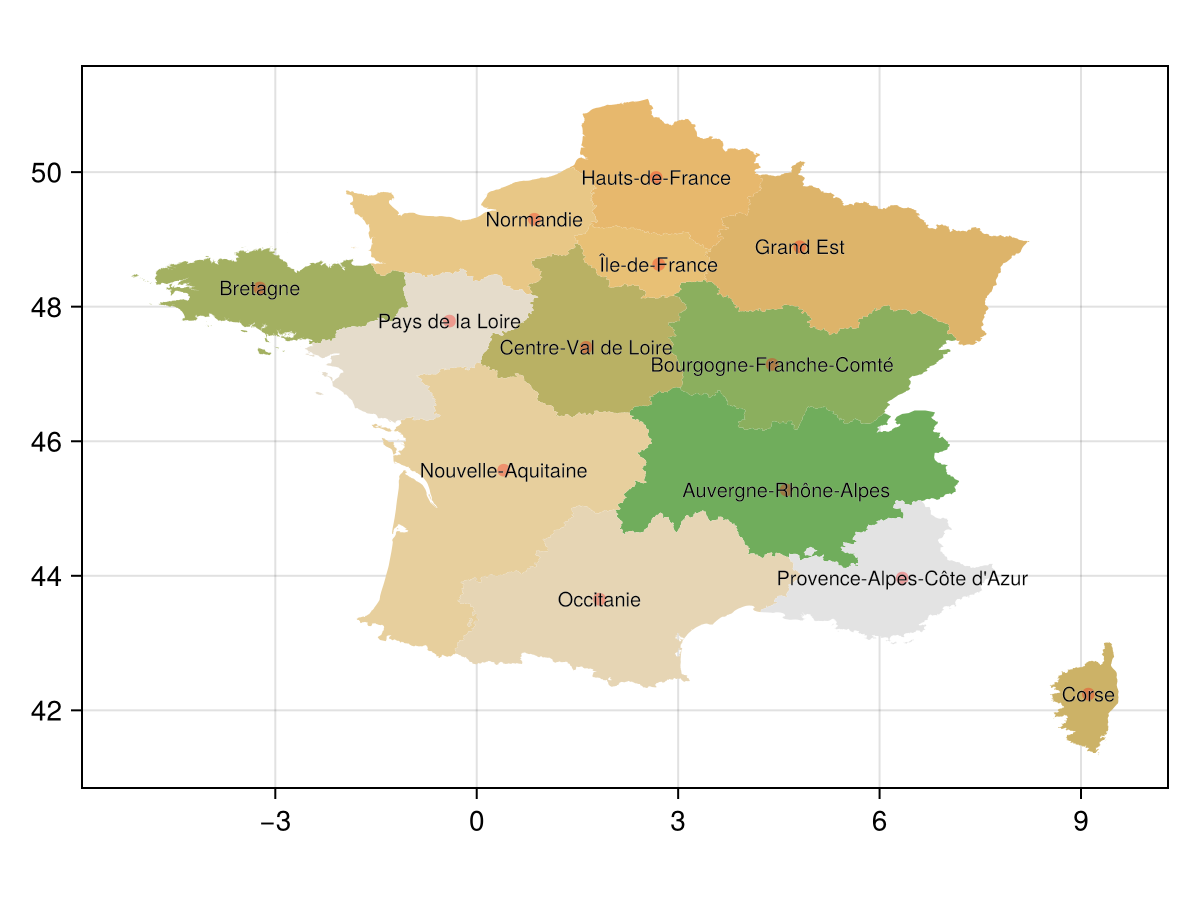

Just for context, let's also plot the centroids:

using GeometryOps: centroid
centroids = centroid.(fra_states.geom)
scatter!(a, centroids; color = (:blue, 0.3))
f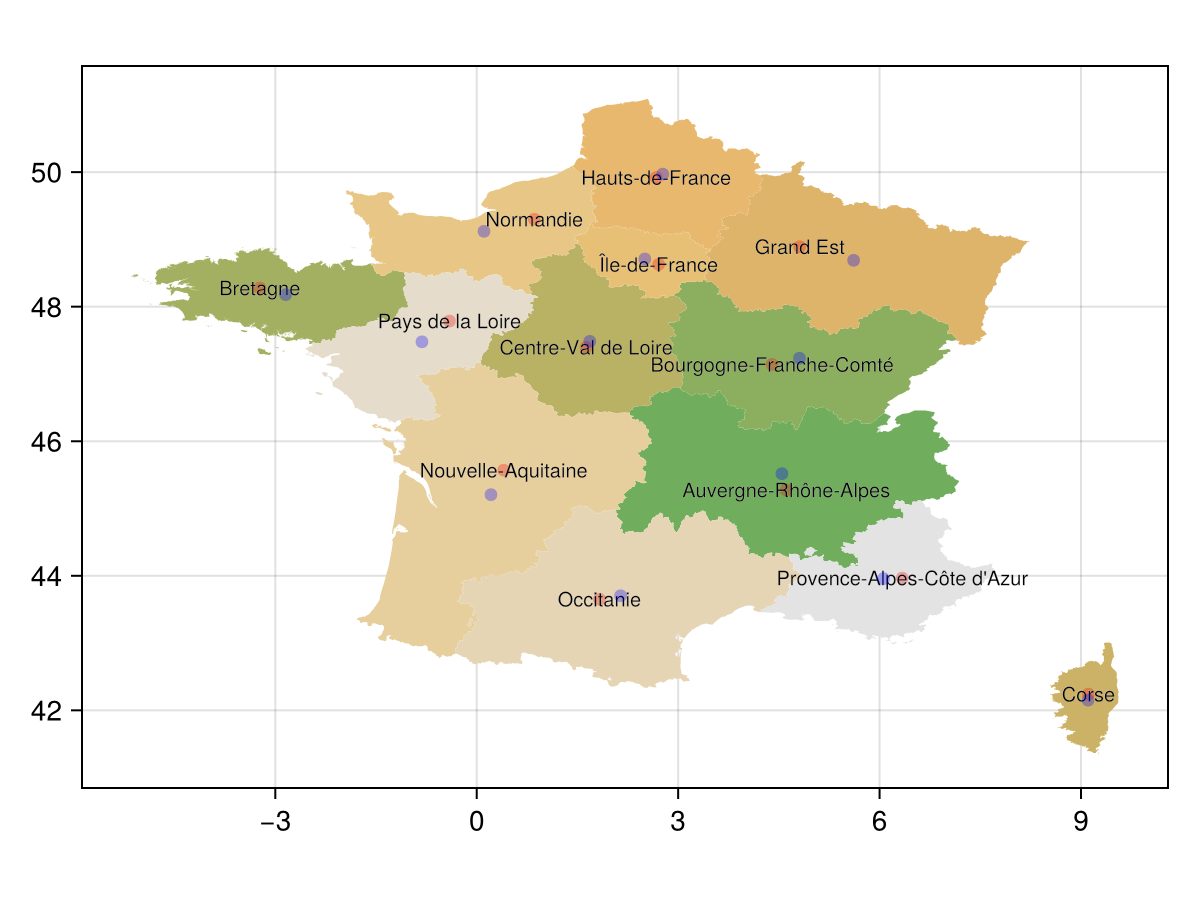

Note that here, in Corsica, if we placed the label at the centroid then it would have spilled out of the polygon. These situations are where Polylabel comes in handy!

It's always ideal to compute the polylabel in the projection you are targeting, since the shape of the polygon changes depending on the projection you use as well as the aspect ratio of your axis.

This isn't restricted to geospatial data in any way - labeling samples segmented from a microscope image is also very possible!

# Polylabel.polylabel — Function.

polylabel(polygon; rtol = 0.01, atol = nothing)::Tuple{Float64, Float64}

polylabel finds the pole of inaccessibility (most distant internal point from the border) of the given polygon or multipolygon, and returns its coordinates as a 2-Tuple of (x, y).

Any geometry which implements the GeoInterface.jl polygon or multipolygon traits can be passed to this method.

This algorithm was originally written (and taken from) mapbox/polylabel - you can find a lot more information there! To summarize, the algorithm is basically a quad-tree search across the polygon, which finds the point which is most distant from any edge.

The algorithm is iterative, and the tol keywords control the convergence criteria.

rtol is relative distance between two candidate points, atol is absolute distance (in the same vein as Base.isapprox). When atol is provided, it overrides rtol. Once a candidate points satisfies the convergence criteria, it is returned.

source